Traveling Salesman Approach to Visiting Data-loggers

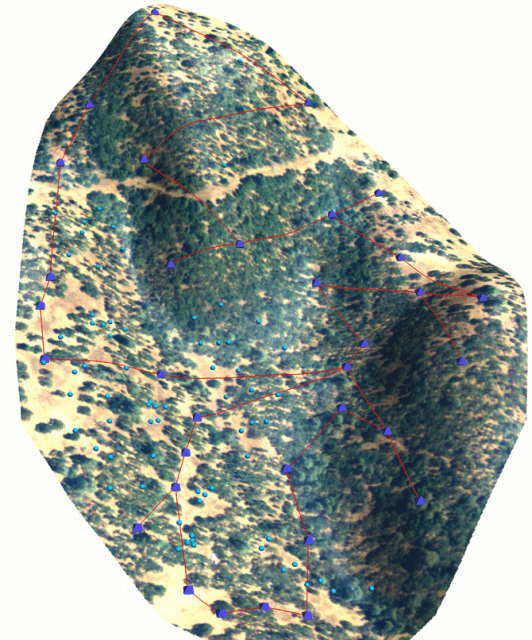Premise:
Several data-loggers in steep terrain; how can we visit all of them in the most efficient manner such that we traverse the least cumulative slope gradient? In a sense this is a traveling salesman style problem, with travel costs defined by slope gradient. The v.net.salesman module in GRASS can be used to compute the optimal route between data-loggers, given: 1) a network of lines connecting all points to be visited and 2) transferal of slope cost information to the network. An example approach is listed below. Note that due to a bug in v.net.salesman, we need to use one extra step-- details below.

Approach:

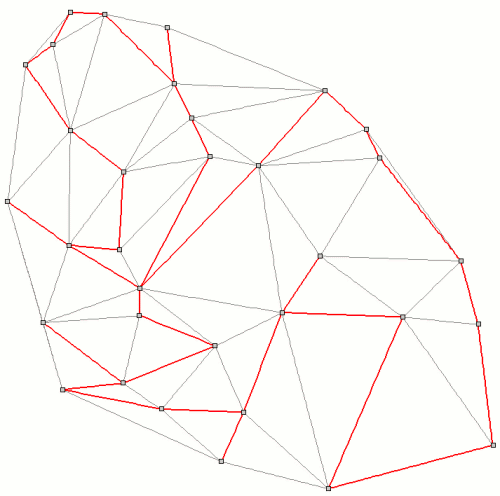
1. generate a delaunay network between points
2. densify the line segments along the network (v.split)
3. convert the network to a 3D, by sampling a DEM along vertices (v.drape)
4. save the slope of each line segment on the network to its attribute table (v.to.db)
5. use the squared slope as the travel cost
6. re-connect the new attribute table from the 3D map, to the original 2D map (v.db.connect)
7. connect data-logger points to delaunay network (v.net)
8. solve the traveling salesman problem (v.net.salesman)

 
Room for Improvement:

1. generate a cost surface using a combination of slope map and known walkable trails / roads
2. add support for lines to v.what.rast -- this would allow us to sample a more realistic cost surface, generated with r.cost
3. fix v.net.salesman so that it can use 3D input maps

Optimal Datalogger Route

mplementation in GRASS:

# generate simple network connecting all points
v.delaunay --o -l in=temperature_sites_maybe out=tri

# densify line segments
v.split --o in=tri out=tri_2 length=5

# add categories
v.category --o in=tri_2 out=tri_3 option=add type=line

# convert to 3d, using our elevation model
v.drape --o in=tri_3 out=tri_4 rast=rtk_elev_var_smooth@rtk

# add a table
v.db.addtable map=tri_4 columns="cat integer, cost double"

# use the slope between line segments as the cost
v.to.db map=tri_4 type=line layer=1 option=slope columns=cost

# make all slopes positive
echo "UPDATE tri_4 set cost = cost * cost" | db.execute

# connect table from 3D map to original 2D map:
v.db.connect map=tri_3 table=tri_4

# make a copy, which brings over a copy of the linked table
g.copy --o vect=tri_3,triangulation

# clean-up
g.remove vect=tri,tri_2,tri_3,tri_4


# make a network
v.net --o in=triangulation points=temperature_sites_maybe out=net --o operation=connect thresh=10

# check network-- has categories?
v.category net op=report

# solve traveling salesman problem
# does not work with 3D maps (ticket # 406)
v.net.salesman --o in=net out=salesman acol=cost ccats=1-33

Links:

Spatial Clustering of Point Data: Spearfish Example

Vector Operations

Traveling Salesman Approach to Visiting Data-loggers II