Home » Software » GRASS GIS: raster, vector, and imagery analysis » Raster Operations » Using R and r.mapcalc (GRASS) to Estimate Mean Topographic Curvature

Using R and r.mapcalc (GRASS) to Estimate Mean Topographic Curvature

Aug 3, 2010 metroadmin

Recently I was re-reading a paper on predictive soil mapping (Park et al, 2001), and considered testing one of their proposed terrain attributes in GRASS. The attribute, originally described by Blaszczynski (1997), is the distance-weighted mean difference in elevation applied to an n-by-n window of cells:

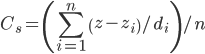chart.png Equation 4 from (Park et al, 2001)

where n is the number of cells within an (odd-number dimension) square window excluding the central cell, z is the elevation at the central cell, z_{i} is the elevation at one of the surrounding cells i, d_{i} is the horizontal distance between the central cell and surrounding cell i. I wasn't able to get a quick answer using r.neighbors or r.mfilter, so I cooked up a simple R function to produce a solution using r.mapcalc. The results are compared with the source DEM below; concave regions are blue-ish, convex regions are red-ish. The magnitude and range are almost identical to mean curvature derived from v.surf.rst, with a Pearson's correlation coefficient of 0.99. I think that it would be of general interest to add functionality to r.neighbors so that it could perform distance-weighted versions of commonly used focal functions.

Elevation surface (left) and resulting mean curvature estimate (right)
Figure: Elevation surface (left) and resulting mean curvature estimate (right)

References

  • Blaszczynski, J. Landform characterization with geographical information systems Photogrammetric Engineering and Remote Sensing, 1997, 63, 183-191
  • Park, S.; McSweeney, K. & Lowery, B. Identification of the spatial distribution of soils using a process-based terrain characterization Geoderma, 2001, 103, 249-272

Implementation and example usage in R

## assumes square pixels
## i.e. EWres = NSres
f <- function(rast.in, rast.out, file=paste(rast.out, '.mapcalc', sep=''), n=5, res=1)
        {
        # the matrix must be an odd number of rows / cols
        if(n %% 2 == 0)
                stop('n must be an odd number')
       
        # init a matrix to evaluate our filter on
        x <- matrix(1:n^2, nrow=n, ncol=n)
       
        # where is the center of the matrix
        x.center.offset <- median(c(1:n))
       
        # generate an offset from the center of the matrix
        the.offset <- c(rev(1 - 1:x.center.offset), 1:(x.center.offset-1))
       
        # convert into matrix of row and collumn-wise offsets
        # according to GRASS's r.mapcalc syntax
        row.offset.mat <- matrix(rep(the.offset, n), nrow=n, byrow=FALSE)
        col.offset.mat <- matrix(rep(the.offset, n), nrow=n, byrow=TRUE)
       
        # compute linear distance from center
        # we are assuming the EW and NS resolution is constant
        dist.mat <- sqrt((row.offset.mat * res)^2 + (col.offset.mat * res)^2)
       
        # generate script
        e <- paste('((', rast.in, ' - ', rast.in, '[', col.offset.mat, ',' , row.offset.mat, ']) / ', dist.mat, ')', sep='')
       
        # remove reference to center cell
        e <- e[-median(1:n^2)]
       
        # generate sum
        e.sum <- paste(e, collapse=' + ')
       
        # add final syntax, along with final division by number of cells - 1
        e.final <- paste('Cs = ( ', e.sum, ') / ', signif((n^2)-1, 2), '.0', sep='')
       
        # write out to file
        cat(e.final, file=file)
        }
# example usage
f(rast.in='rtk_elev', rast.out='Cs', n=5, res=1)
X

Resulting r.mapcalc input for a 5x5 window

Cs = ( ((rtk_elev - rtk_elev[-2,-2]) / 2.82842712474619) + ((rtk_elev - rtk_elev[-2,-1]) / 2.23606797749979) + ((rtk_elev - rtk_elev[-2,0]) / 2) + ((rtk_elev - rtk_elev[-2,1]) / 2.23606797749979) + ((rtk_elev - rtk_elev[-2,2]) / 2.82842712474619) + ((rtk_elev - rtk_elev[-1,-2]) / 2.23606797749979) + ((rtk_elev - rtk_elev[-1,-1]) / 1.4142135623731) + ((rtk_elev - rtk_elev[-1,0]) / 1) + ((rtk_elev - rtk_elev[-1,1]) / 1.4142135623731) + ((rtk_elev - rtk_elev[-1,2]) / 2.23606797749979) + ((rtk_elev - rtk_elev[0,-2]) / 2) + ((rtk_elev - rtk_elev[0,-1]) / 1) + ((rtk_elev - rtk_elev[0,1]) / 1) + ((rtk_elev - rtk_elev[0,2]) / 2) + ((rtk_elev - rtk_elev[1,-2]) / 2.23606797749979) + ((rtk_elev - rtk_elev[1,-1]) / 1.4142135623731) + ((rtk_elev - rtk_elev[1,0]) / 1) + ((rtk_elev - rtk_elev[1,1]) / 1.4142135623731) + ((rtk_elev - rtk_elev[1,2]) / 2.23606797749979) + ((rtk_elev - rtk_elev[2,-2]) / 2.82842712474619) + ((rtk_elev - rtk_elev[2,-1]) / 2.23606797749979) + ((rtk_elev - rtk_elev[2,0]) / 2) + ((rtk_elev - rtk_elev[2,1]) / 2.23606797749979) + ((rtk_elev - rtk_elev[2,2]) / 2.82842712474619)) / 24.0
X

Links:

Simple Comparison of Two Least-Cost Path Approaches

Raster Operations

Visual Comparison of 2 Raster Images